指数爆炸's Notes

Appearance

散列表（哈希表） ​

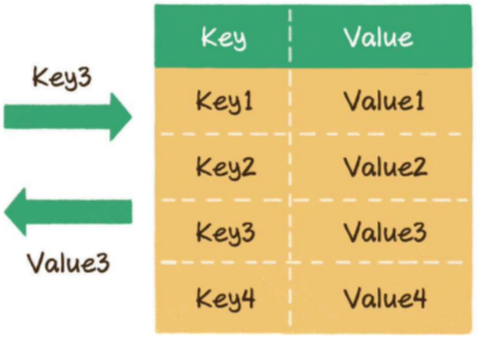
[!quote] 散列表 散列表 本质是一个数组，提供了 key 和 value 的对应关系【只要给出 key 就马上可以找到 value，时间复杂度为 O(1)】 300

填装因子 ：填装因子 = 关键字个数 / 散列表长度

散列表的原理 ：散列表本质是一个数组，而哈希函数就是将 key 与数组下标转换的桥梁

mermaid
graph LR
	f[用户]--拿着-->a
	a[key]--经过-->b{哈希函数}
	b--生成-->g[哈希值]
	g--进行-->h{取模/位运算/……}
	h--变成-->d[数组下标]
	d--通过-->z[数组]

	z--拿到-->e[value]--返回给-->f

哈希冲突 ​

[!quote] 哈希冲突

哈希冲突 就是两个不同的 key 经由哈希函数转换取模后，出现的数组下标相同的冲突

mermaid
graph LR
a[key1]-->c{哈希函数}-->d[哈希值]-->e{取模……}
b[key2]-->c-->d-->e
e-->f[数组下标]

解决办法：

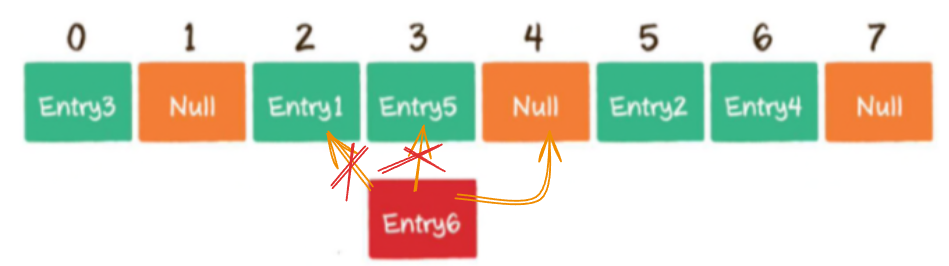
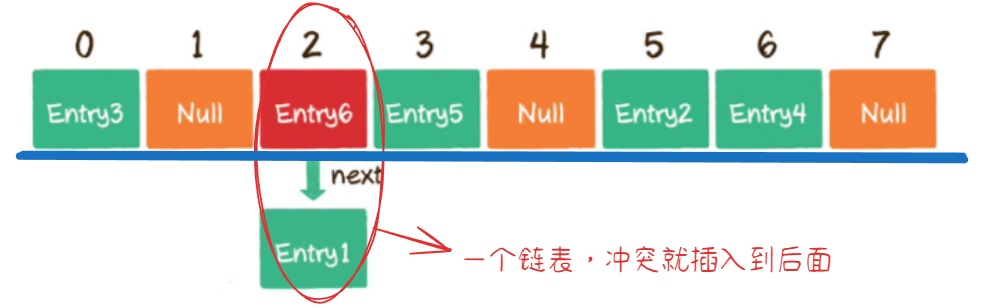
  • 开放寻址法：冲突后，就从冲突位置往后找空位插入【应用于 ThreadLocal】 500
  • 链表法 / 拉链法：冲突后，把冲突的位置当成是链表的头结点【应用于 HashMap 中】 500
  • 再哈希法：同时构造多个哈希方法，第一个方法重复后，再哈希第二个方法
  • 建立公共溢出区：建立一个区域供所有冲突的元素放，这个区域又可以叫溢出表，没有发生冲突的放在基本表里

写操作 ​

读操作 ​

  • 通过哈希函数，将 key 转换为数组下标
  • 根据数组下标找到对应的元素，看看 key 是否正确匹配【意味着哈希表的每个槽位都存储一个 key，一个 value】
    • 如果正确，那就找到了
    • 如果不正确，那就顺着该位置的链表，往下继续匹配

扩容 ​

什么时候需要扩容 ?

当 HashMap.size >= Capacity * LoadFactor

  • HashMap.size ：总长度
  • Capacity ：当前长度
  • LoadFactor ：负载因子，默认是 0.75
  • 创建一个新的 Entry 空数组，长度是原来的 2 倍
  • 由于数组长度不同，所以哈希规则也不同，遍历原 Entry 数组，重新 Hash 到新数组